赫德数学公开课:通过一节颠覆性的数学课,我们找到了让孩子爱上数学的窍门!
我们可能很难想象,一个上一秒还在打趣着说“数学有点无聊”的孩子,在上过一堂“全景式数学”课后,就意犹未尽地感慨道,“数学真神奇,希望再多上几节!” 这一有趣的转变就发生在12月9日的“赫德之光”大师讲堂活动中,全国著名特级教师、“全景式数学”的首创者张宏伟老师来到了上海赫德双语学校,以“公开课+讲座”的形式,带孩子们领略了不一样的数学魅力。
It may be hard to imagine that a child complaining of the boredom of mathematics suddenly becomes interested in the discipline and desires to have more mathematics lessons. It is not a fairy tale, but a real scene from the latest HD Illumination event, where Mr. Hongwei Zhang, one of the most prestigious mathematics teachers in the country, paid a visit to HD Shanghai and gave a class for the students. As the initiator of Panoramic Mathematics Education, Mr. Zhang is dedicated to exploring innovative mathematics learning and teaching methods in primary education. He shared his insights at the event and thus left a deep impression on parents and teachers.

一堂别开生面的数学课
将一张纸首尾相连形成一个圈,你会怎么做?
在听到张老师的提问后,上海赫德双语学校的孩子们纷纷行动了起来,有人将纸条从头到尾理平整,然后顺着围成了一个圈,也有孩子将纸条拧了一次,同样首尾相连形成一个圈。
看到孩子们的行动,张老师笑了:“孩子们,你们很棒!想到不仅可以从正面围成一个圈,还想到了从反面入手!” 事实上,从反面入手围成的一个圈,正是张老师今天想要带孩子们探讨的主题——
莫比乌斯圈。


莫比乌斯圈,是由德国数学家、天文学家莫比乌斯和约翰·李斯丁在1858年独立发现的。这个结构可以用一个纸带旋转半圈,再把两端粘上之后轻而易举地制作出来,它也是一种重要的拓扑学结构。
当然,在小学数学的课堂上,张老师并不会照本宣科地讲授拓扑学的高深知识,只见他神秘一笑,拿起一把剪刀:“孩子们,请你们把从正面和反面分别围成的纸圈从中间剪开,看看会变成几个圈?”



话音刚落,孩子们就纷纷行动了起来,不一会儿,惊喜的呼声充斥了整个课堂。原来,“正圈”从中间剪开后,会自然而然地变成两个圈;而拧一次后围成的”莫比乌斯圈“,却在剪开后变成了一个圈!
”太神奇了!怎么会这样呢?“
在孩子们的热情与好奇之中,张老师继续引导大家思考——现在我们知道,将“正圈”从中间剪开,会得到两个圈;而将”莫比乌斯圈“从中间剪开,会得到一个圈,那么如果我们将一张纸带拧两次后围成一个圈,再从中间剪开,会得到几个圈呢?

“一个!”、“两个”、“四个!”……孩子们猜测的声音不绝于耳,但事实上,大部分孩子只是凭着主观臆断在做一些推测,而没有切实的根据。
张老师把话筒递给上海赫德双语学校的家长们,依旧得来了一些不确定的猜测答案。这时,张老师拿起了拧两次后制作而成的纸圈,从中间剪开,答案,很快就清晰地呈现在了他的手中——两个圈!


课堂进展到这里,气氛已经变得热烈无比,一个孩子率先举手提问,如果把一个拧了三次、再围成的纸圈从中间剪开,那么会得到几个圈?
听到孩子的疑问,张老师的眼睛亮了,他在黑板上写下几个大字“数学的猜想”,原来,“数学的猜想”和“瞎猜”的不同之处,就在于我们要学会对自己所做的事进行联想与追问,进行反思,一边反思,一边将它们记录下来加以观察,看看是否会从中找到什么规律。此时,再依据规律去进行猜想,这才是“数学的猜想”!

有了张老师这样的引导,有关莫比乌斯圈的一个最简单的规律正缓缓浮出水面——一次都不拧,从中间剪开后是两个圈;拧一次,从中间剪开后是一个圈;拧两次,从中间剪开后是两个圈……
2、1、2、1……那么拧三次,从中间剪开后,会是一个圈吗?张老师拿起了剪刀,验证了这种“数学的猜想”,果然,拧三次的圈剪开后,得到了一个圈!
这,也正是张老师给孩子们带来的拓扑学启蒙。通过不断的猜想与验证,孩子们的空间思维能力得到了极大的锻炼;同时,通过这样一节数学课,张老师还希望教会孩子们这样一些道理:
首先,当我们做一件事的时候,可以正着做,也可以反着做,而当我们反着做的时候,往往就会收获很多意想不到的新发现;
其次,当我们看到1的时候就可以想到2,看到2的时候可以想到3,见南可以追北,见语文可以追数学,这是最不可或缺的联想与追问能力;
最后,通过之前所提到的“反思-记录-观察-找出规律-做出猜想”等一系列步骤,我们终将学会“数学的猜想”,它与胡猜乱想有着天壤之别,更是孩子们终生受用的关键能力与核心素养。当然,在这个过程中,孩子可能猜错,大人可能猜错,数学家也可能猜错,可是猜错并不妨碍我们的探索精神和对数学之美的享受,反而给孩子们带来了一种学习上的安全感,其背后正是积极而无畏的数学精神。

一堂颠覆性的数学课结束后,孩子们个个都露出了意犹未尽的神情。原先打趣着说“数学无聊”的孩子叫嚷着要再多上几节数学课,而原本喊着希望这节课“不留作业”的孩子,则开开心心地主动提出:“我要回家做数学作业了!” 美妙的转变,就在顷刻之间发生,这就是激发孩子对数学的兴趣与好奇心的魅力,孩子们看见的,是一种完全不一样的数学教育。
在后续的讲座中张老师也提到,其实他并不指望每个离开课堂后的孩子,将来都能成为这方面的专家;但只要能给孩子们埋下一颗种子,只要将来能有一颗种子生根发芽,那么作为教师,就是最幸福的事。
揭开全景式数学的面纱
一节看似很像手工课的数学课结束,张宏伟老师在上海赫德双语学校开展的生动活泼的课堂形式收获了大家阵阵的掌声,而在掌声中,“全景式数学”的面纱也被揭开。
我们都知道,在摄影中有一种技术叫“球形全景摄影”,利用这种技术呈现出来的图片,可以让人们360度无死角地认识世界。同理,“全景式数学”也是一种让学生360度无死角地认识数学、认识世界的数学学习方式,它是一种基于世界的数学、历史与文化来完善与丰富的数学课程,通过它构建的数学世界,是丰富的、广角的,也是完整的;学生的思考空间也是完全敞开的,是发散的,是自由的。
在后续的观点报告中,张老师从五个方面向我们进一步揭开了“全景式数学”的奥秘。
No.1
内容的补充和完善
还记得我们以前,是如何学习四边形的吗?
事实上,一些传统的数学课本已经很贴心地将四边形帮我们罗列好了。但有时,正是由于课本过于“贴心”,以至于在一定程度上限制了学生的思路。
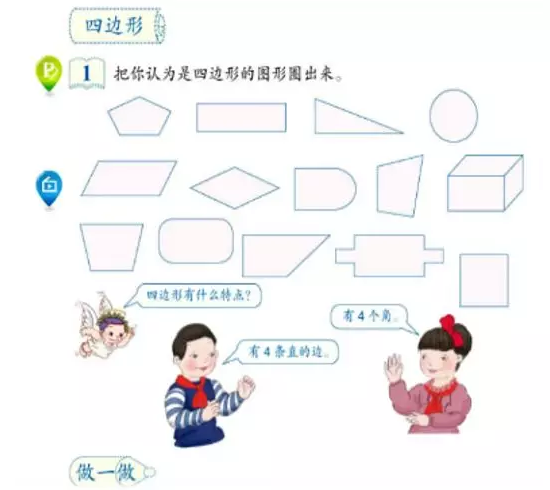
张老师提到,在小学阶段的数学学习中,我们大多接触的是平面四边形中的凸四边形,而未曾涉及凹四边形的概念,空间四边形更是丝毫没有提及,以至于当他拿着另外两种四边形的示意图去询问学生时,很多孩子都一脸茫然地表示——这应该不是四边形。
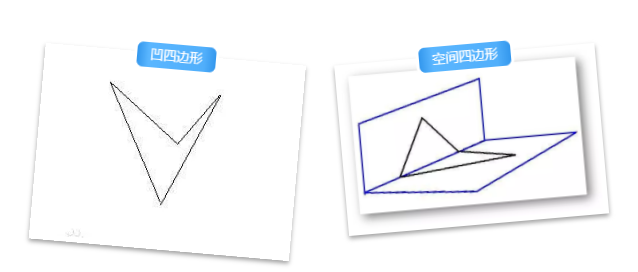
如果在孩子们的概念中,四边形只是等同于“平面四边形中的凸四边形”,那将是一件多么可惜的事呀!对此,张宏伟老师仅仅在课堂上引入了一个灵活可翻转的教具,一下就将学生的思路打开了。

当然,除了对传统教材中不够完善的地方加以补充,在全景式数学的课堂中,张老师还对非传统的数学内容进行了引进和编排。在此次公开课上呈现的拓扑学启蒙,就是一个生动形象的例子,通过这样的努力,张老师希望达成三个目的——
丰富学生数学视野;
完整对数学的认识;
完整对世界的认识。


说起来似乎很容易,可为了达至这些目标,需要教师时时开动脑筋,付出持之以恒的努力。
No.2
学习方式的变革
我们常说,数学是一门需要动脑子的学问,好像只有那些脑筋开动得够快的孩子,才能学好数学。可在张宏伟老师看来,数学不仅是大脑的学问,更是”四肢“、是”肠胃“的学问,当孩子们调动各种各样的感官,在一个真实的世界中与数学邂逅,又何愁学不好数学呢?
学习分数,张老师拿来了一块蛋糕,请同学们均等地分成四份,再请大家分别吃掉其中的四分之一、四分之三,在鼓囊囊的腮帮子中,孩子们自然而然地感受到,四分之三多于四分之一。此时,与其说孩子吃掉的是蛋糕,还不如说是”分数与分数的大小“。

学习圆柱体的侧面积,张老师带孩子们来到了沙坑,每个小组自制一台压路机,通过实地操作,让孩子们感知圆柱体的侧面积究竟该如何计算。等孩子们满身沙子地从外面回来,再写下计算公式,张老师可以肯定,这个知识是他们自发习得的,而非灌输。
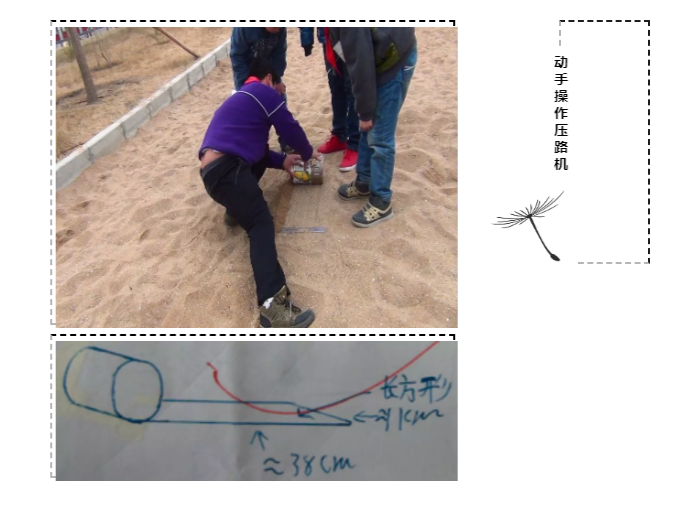
在”全景式数学“的课程理念中,孩子们的学习时空被重构,他们将在生活中解决原态的真实问题,学活的数学,活学数学。此时,数学不再是课本或考卷上那一道道冰凉的题目,而是鲜活的世界,是他们每天都在与之产生联结的现实。
No.3
学习现实的重建
在传统的数学课本上,这样的题目并不少见:
甲乙两人合资开了一个文具超市。甲乙投入资金的比例是2:5,年终一共盈利28万元,甲乙应该如何分配这笔钱?
可在孩子们幼小的心灵里,其实会盘旋着这样一个“灵魂拷问”——甲乙分钱,和我有什么关系?
顺着孩子们的童趣心理,张老师提出要重建他们的“现实”,这包括孩子的生活现实、学习现实及各门学科的现实。通过这样的方式,我们能够做到将数学巧妙融入到好玩的、无形的非数学活动中,数学也最终从“目的”变为了“工具”。

还是同样的按比例分配的问题,这次,张老师带大家来玩转和音。一个铁盒,一个橡皮筋,通过这样简单的工具,孩子们制作出了一种简单的“乐器”,然后通过弹奏“乐器”两边的“琴弦”,来看看当它们处于一个怎样的比例之时,和音最为和谐。
几次试验下来,孩子们自然而然地发现了和音比——1:1,这是同音;1:2,这是八度;2:3,这是纯五度;3:4,这是纯四度……为了演奏出好听的乐曲,孩子们自己动笔,算起了长度比例。
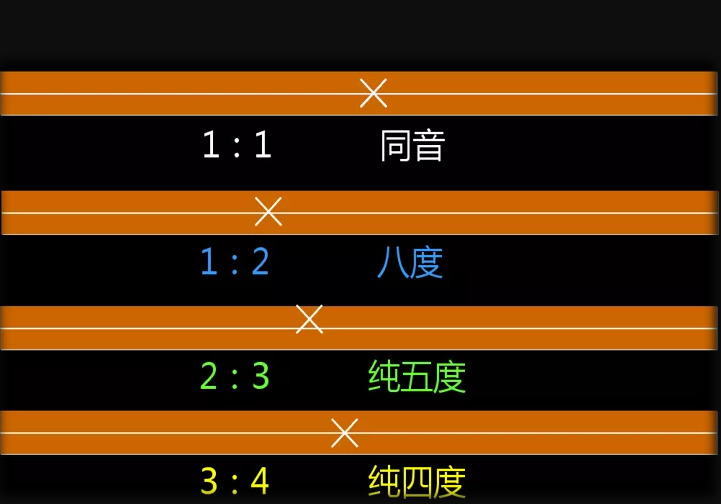
数学知识,早已演变为孩子们演奏出美妙乐曲的方式与途径,在全景式数学中,还有太多这样跨领域的融合性项目课程,通过对现实的重建,我们还原了数学的本真——一种探索与发现的工具。
No.4
历史文化的还原
我们在学习文科类科目时,时常会涉及到相关历史文化的习得,数学也不例外。张宏伟老师认为,真正的数学教学,应该是数学的历史文化、知识技能、思想方法三位一体的统一。换言之,如果把数学放在一个历史文化的语境中去学习,将更加有益。
函数,我们大家都学过,可要问函数中的这个“函”是什么意思,恐怕大多数人都一头雾水。而在张老师的课堂上,从一年级开始,其实就已经可以在潜移默化之中,结合历史文化来解构这个概念。
下面的练习题我们都很熟悉,这是小学低龄段一定会学习的加法运算。可如果这个时候,教师提一句,随着加数的变化,和会发生怎样的变化?其实许多学生都会本能地感觉到,和会随着加数的改变,发生相应的改变。这就是函数最基础的概念,而这里的“和”,也可以理解为“含有一个变数的式子”,又或者可以直接简称为“含数”。
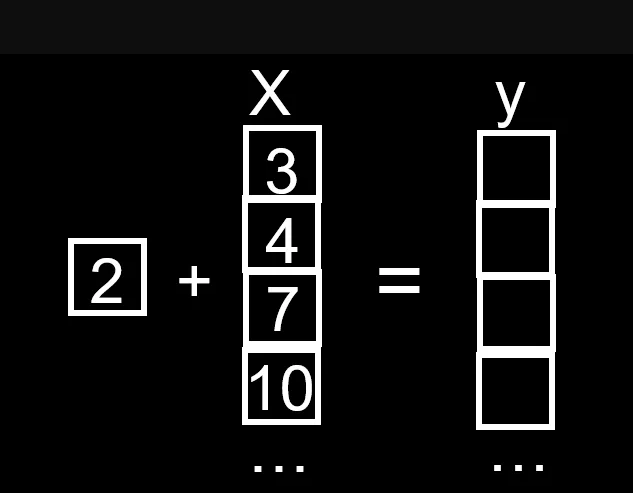
清朝数学家李善兰曾这样给出函数的定义:“凡式中含天,为天之函数。” 其背后对于函数的定义与理解完全相通,而当张老师提及,在中国古代,“含”与“函”为通假字时,在座的许多老师和家长都露出了恍然大悟的神情,这就是回溯历史文化的重要性。
No.5
思考力培养的完善
常言道,“师傅领进门,修行在个人”。可对于全景式数学来说,最怕的其实就在于师傅总是“领进门”,而不告诉学生,自己该如何找“门”。
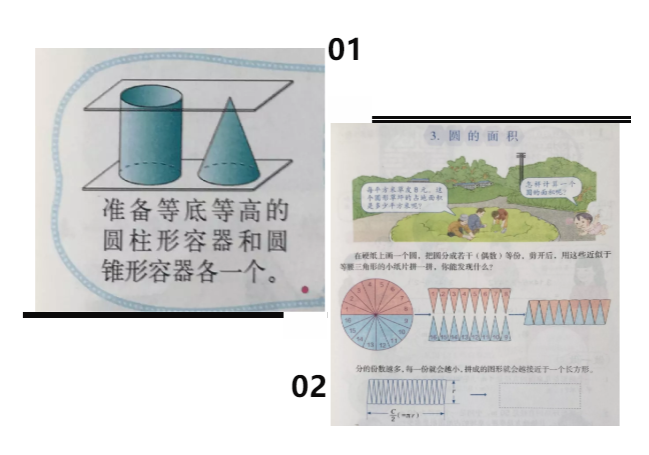
以上,其实都是过分强调“领进门”的典型案例,可“等底等高”、“分成若干(偶数)等份”这些重要的操作步骤,其实都是教材直接告知学生的,而非学生自己通过探索得来。
在全景式数学中,最重要的就是补足数学学习中不可或缺的触发和定向阶段,对课程和教学的结构、流程、评价方式等进行相应的变革,通过这些重建,把孩子培养成将来无论面对怎样的问题,都能够自己找到“门”的人。与仅仅教授数学知识相比,对数学智慧的传授,才是更高层面的教育目标。


短短两个小时的全景式数学公开课与讲座,或许无法让每个参与其中的孩子、每位前来听讲的大人都深刻而全方位地感知其魅力。但从课堂上孩子们踊跃的发言与时不时举起的小手中,我们可以感受到,这就是全景式数学教育的奇妙之处。它是一种全人理念下的数学教育,通过教授知识,通达人生智慧,所指向的是孩子的全面发展和应对未来挑战的能力。
推荐阅读:



